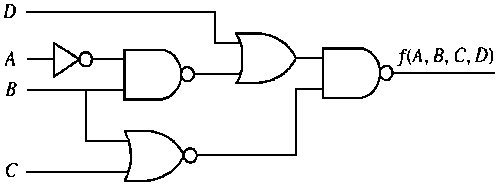
Obtain the equation of the boolean function f implemented in the following logic diagram in standard POS and SOP forms and show that they are the same.

Suggested approach --
Write the Boolean equation for f directly (with lots of parentheses and without any simplifications),
simplify the equation algebraically to eliminate all parentheses except the outer most pair that result from the final NAND gate (the equation should have 3 terms, 1 with 2 literals and 2 with 3 literals and a prime outside the parentheses),
make a truth table for f' (the equation obtained in step 2).
add a f column to the truth table by simply inverting the f' column,
use the completed truth table to obtain the K-map for f,
loop the ones in the map to get f and the zeros in the map to get f' both in SOP form and, finally,
invert f' and apply DeMorgan's Law to get f in POS form.
The POS and SOP forms of functions are generally different. This function has identical POS and SOP forms because the terms in the SOP form each contain just a single literal which is equivalent to saying there is only one loop of zeros on the K-map.