Copyright © 2020-21
Robert W. Hasker

CS 3040 - Note: Exam 1 Review

Readings

• Software Languages: Ch. 2
• Real World Haskell: Chs. 1 and 2

You are allowed one page of notes for the exam. The exam will be delivered through Canvas but students will take it during the class hour.

Review questions (for reference only - the exam may include other topics!):

Questions

1. Explain when a finite state machine accepts its input.
2. Explain when a finite state machine rejects its input.
3. Circle the strings accepted by the following DFSM: a, aa, abbc, bc, bbc, bbcc, abc, abcca, ac, acccaa, one, two, three, ababbabc, cccc, aaacc, abcabc, abbbaabc
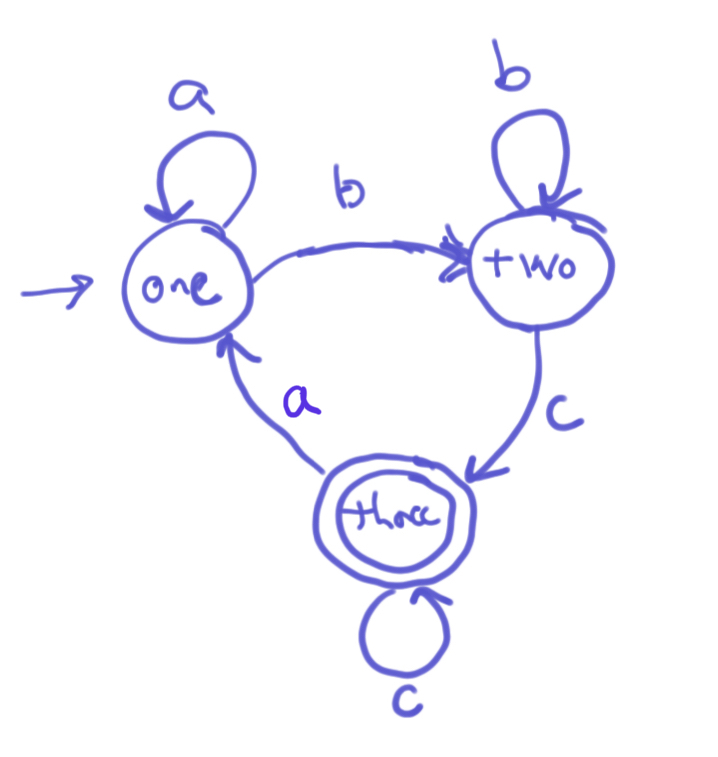
4. What is the regular expression accepted by the above DFSM?
5. Does the above DFSM accept any strings with infinite length?
6. Suppose we have built an incorrect FSM for a particular problem. What is the best way to prove that the machine contains errors?
7. Explain the difference between deterministic and non-deterministic FSMs.
8. What would it mean for an FSM to have no final states?
9. Draw a (deterministic) FSM accepting birth years in 1900 to the present. Show each possible input as a separate transition.
10. Draw a FSM for a machine that sells cans of pop for 25 cents. Assume the user deposits nickles, dimes, and quarters, and do not allow more than 25 cents to be deposited. Dispense the pop (whatever is in the machine - the user doesn't get to pick!) when the user clicks the "dispense" button. Clicking a "cancel" button before "dispense" should return any change entered.
11. Why does developing a fluent API start with a step to write (or select) sample programs?
12. Give sample well-formedness conditions for format strings in the language of your choice (C/printf, Python/format, Ruby/interpolation with #)
13. What is the basic goal of ANTLR? What are some of the features it provides that supports that goal?
14. The RE operators + and ? are not required - that is, you can write all regular expressions without using these particular operators. Explain why.
15. Describe the following regular expressions in words. Try to give abstract descriptions; for example, (01)+ could be described as "zero followed by one followed by 0, etc., repeated", but that doesn't cover just 01 and isn't a useful characterization. Better would be "alternating 0s and 1s starting with 0".
    1. 0+|1+
    2. 0x[0-9a-fA-F]+
    3. [a-zA-Z]+[^a-zA-Z]?$
16. Using just BNF, give formal definitions of grammars (as a quadruple <N, T, P, S>) generating the following languages:
    • G1 such that L(G1) = {abc}
    • G2 such that L(G2) = all even length strings of a's; for instance, including aa, aaaa, aaaaaa, the empty string, etc.
    • G3 such that L(G3) = (a | b)*
    • G4 such that L(G4) = all Haskell if expressions (but no other types of expressions) over the single boolean value x. For example, if x then if x then x else x else x.
17. Give a derivation sequence for abba using the grammar you wrote for G3.
18. Give an ambiguous grammar G5 such that L(G5) = L(G3). That is, there are two parse trees for any sentence with at least 2 characters in it.
19. Using the EBNF expression grammar in the notes, give a derivation sequence for (5 + 3) * 7 * 8.
20. Draw a railroad diagram capturing even length strings of a's. (This is harder than would be on the exam; there I might ask what a given railroad diagram accepts.)
21. Explain why Python or Ruby is not a pure functional programming language.
22. Give two examples of code (fragments) that follow the syntactic rules of both Haskell and some scripting language (Ruby, Python) but are only legal in the scripting language.
23. Write Haskell functions for the following:
    • Compute the distance between two points, where the points are represented by pairs of floats; for example,

              distance (1.0, 1.5) (3.0, 2.5)
      

      would return the square root of 5, or approximately 2.236.
    • Compute the maximum of a list of non-negative numbers; treat the largest value in an empty list as 0. If a list is not empty, return the largest of the first item and the largest value in the rest of the list. Note you can use max, but not maximum; the point of the exercise is to write your own version of maximum. Your solution must recurse on the list; do not use built-in functions like filter or fold in your answer. Also note that it is fine if your solution accepts ordered types in general (Ord) rather than just numbers (Num).

Notes from quizzes

• Exercise 1 (in Canvas), strings accepted by the FSM with transitions for a, b, and c and the final state being after an a: Start with accepted strings: a, abca, abcabca, etc. So this is sequences of "bca" after an initial a. The empty string is not accepted. This gives a(bca)*.
• Ex2: RE Tutorial: please review the tutorial portion if you had troubles with Ex3 on REs and FSMs. The tutorial does a good job of identifying the pieces (|, *, [a-z], [0-9], capture groups, etc.) but doesn't show how to put them together to solve challenging problems like particular repeat patterns. Know the notation - what's allowed, what's precisely described by a particular pattern - but also know how to put the notation together to meet a goal.
• Q1 on Grammars:
  • Know what the N, T, P, and S are in a tuple for a Grammar: <N, T, P, S>
  • Be clear on derivation sequences. What is one step vs. multiple steps, and how this relates to a parse tree.
  • Be clear on the definition of L(G): "in L(G)" means "a string that can be generated from grammar G".
• Ex3: REs and FSMs: I will have to post notes on this after all have completed the exercise.